参考：

没那么神秘的快速平方根倒数，给你解释一下这个数是怎么来的_哔哩哔哩_bilibili

问题引入

膜拜一下大佬 orz

1999年，当卡马克在开发《雷神之锤III竞技场》时，需要计算照明和投影的波动角度与反射效果（计算3D图形中的法线向量），不得不使用“浮点运算求平方根倒数”，但这样做的成本极高。因为在 3D 游戏中，计算机每秒要进行数百万次这样的运算。于是卡马克想到了一种快速算法，他选择了一个16进制数字0x5f3759df，然后用牛顿法反复迭代，以求出更精确的近似值。

在上个世纪90年代，还没有足够强大的硬件来专门进行这个操作，所有的计算都需要软件进行，无论是开方操作还是除法操作都是非常缓慢的。这个算法最惊艳的地方是，他把开方操作和浮点数除法操作，变成了整数的移位和减法操作。在这个神奇的操作中，可能诞生了有史以来最著名的 magic number：0x5f3759df。

本文主要解构算法的原理和 magic number 的来由。

它到底有多快？

操作系统：WIN11 23H2

CPU：12th Gen Intel(R) Core(TM) i5-12500H 2.50 GHz

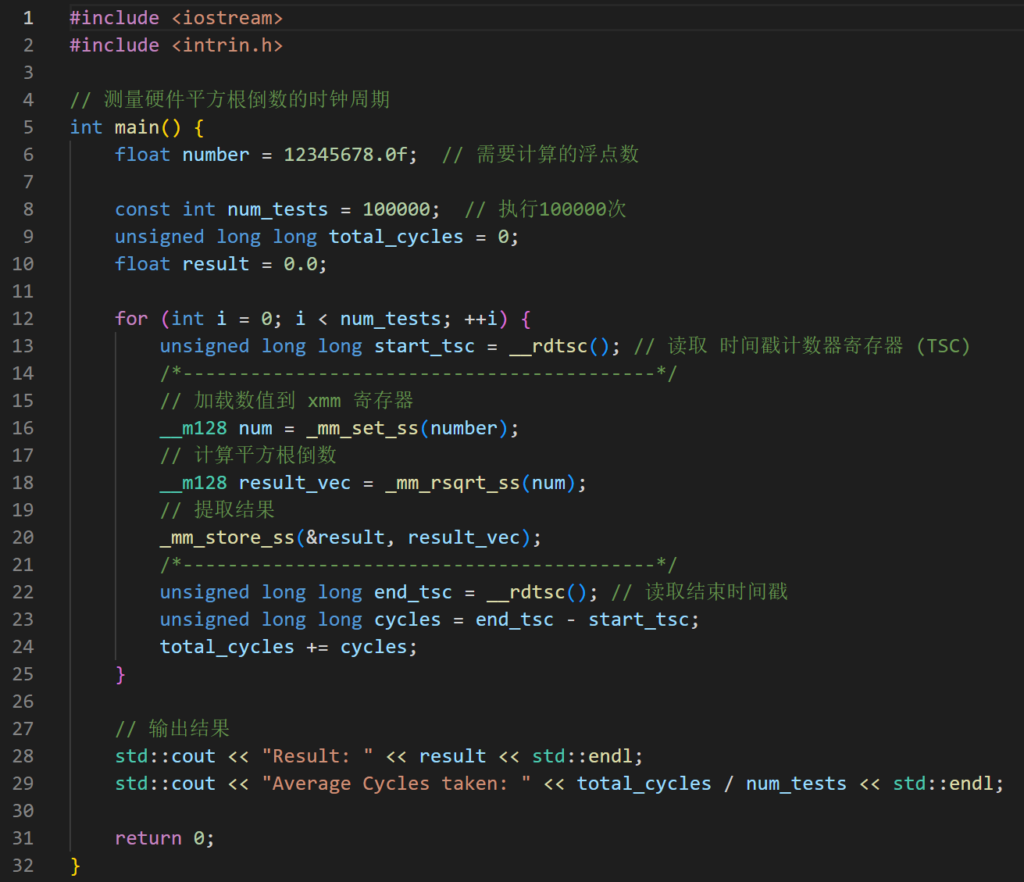
<intrin.h> 是一个头文件，提供了对处理器的特定指令集的访问。它用于访问 CPU 特定功能（如向量运算、内存操作、时钟计时等）的内嵌函数（intrinsics），这些函数直接映射到底层硬件指令。通过其提供的接口，可以：读取时间戳计数器寄存器 (TSC)，得出操作消耗的时钟周期；直接调用硬件计算平方根倒数。

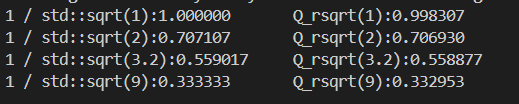
测量快速平方根倒数算法的时钟周期

卡马克的算法，大约在25个时钟周期完成计算。

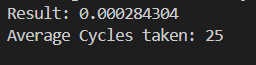
测量硬件平方根倒数的时钟周期

x86机器指令，大约在24个时钟周期完成计算。

该算法在现代还有应用价值吗？

许多现代处理器包含浮点运算单元（FPU），能在硬件层面进行开平方倒数运算，例如前面测试 x86 架构的RSQRTSS指令可以在大约 25 个时钟周期完成计算。RSQRTPS指令可以同时计算四个单精度浮点数，在这类CPU上理应使用机器指令代替软件计算平方根倒数。

但是在FPU性能较弱的处理器，甚至没有FPU的嵌入式处理器中（例如Cortex-M3、Cortex-M0内核的ARM处理器），该算法仍能起到显著的加速效果。

算法的思想

算法的本质其实就是牛顿迭代法（Newton-Raphson Method，简称NR），它是求非线性方程近似根的一种算法，其理论基础是泰勒级数。迭代算法需要输入一个初始近似根 x0，然后根据公式迭代出下一个更加近似的值，不断迭代直到获得满意的精度。

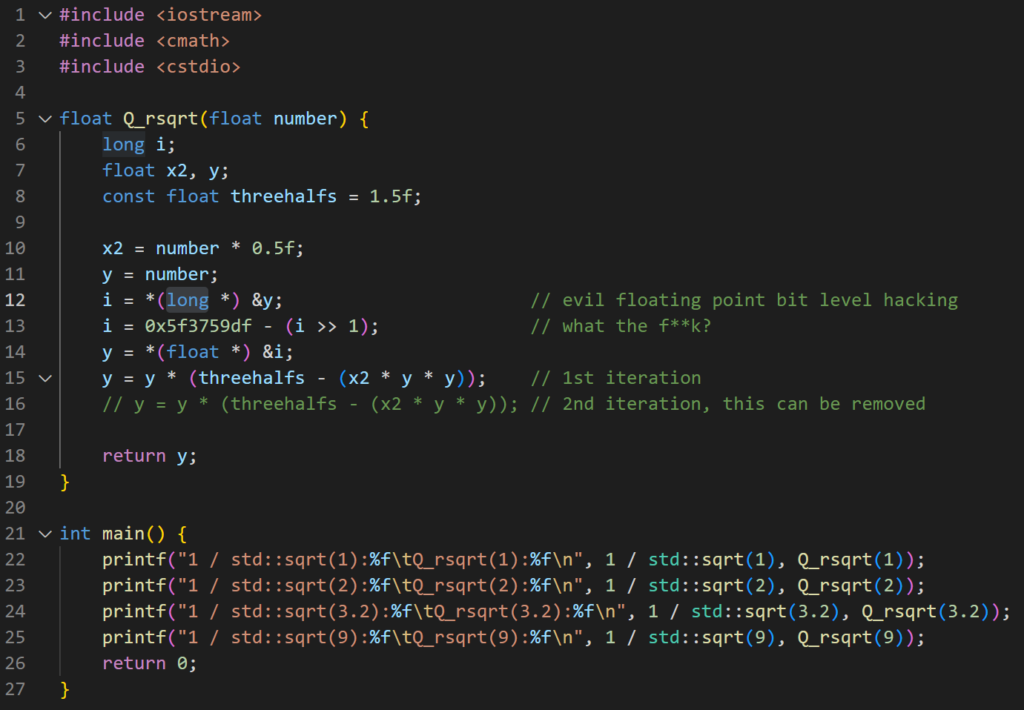
方程 f(x)=0 的第 n+1 代近似根为

$x_{n+1}=x_{n}-\frac{f(x_n)}{f'(x_n)}$

我们可以从函数图像的角度理解牛顿迭代公式：

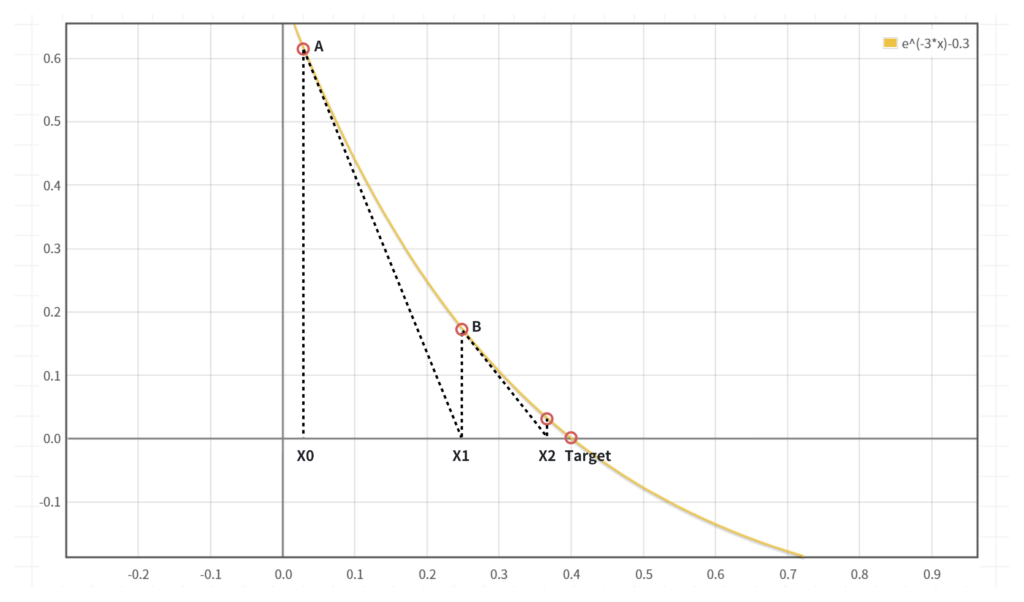
迭代算法的目标是获取 f(x) 图像与x轴交点的坐标，即图中的 Target 点。设定初始近似根为 x=x0，在位置 A(x0,f(x)) 处画一条切线，得到切线与x轴的交点 (x1,0)。x=x1 即新的近似根，x1 比 x0 更接近 Target。依次迭代该过程，最终将得到与 Target 几乎相同的值。

很容易看出，算法收敛的速度与初始近似根 x0 的位置强相关，x0 与真实根的距离越近，算法收敛的越快。magic number 的作用就是估计一个较为准确的初始近似根，以达到加速的目的。

在本问题中，定义如下方程。其中 x 视为一个常数。

$f(y)=y^{-2}-x=0$

利用牛顿迭代法，可以得到下面的迭代式

$y_{n+1}=y_{n}(\frac{3}{2}-\frac{1}{2}xy_{n}^2)$

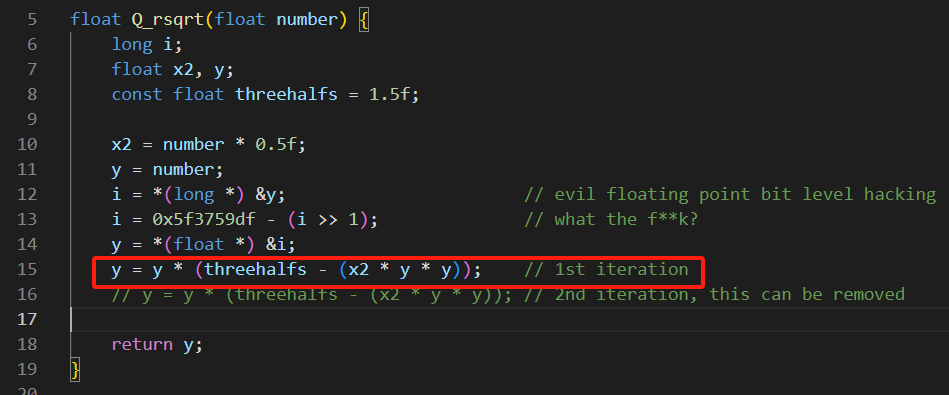
这是算法第15行代码的来由，前6-14行代码用于估计方程第一个近似根y0的值。

magic number 的来由

前文提到，magic number 用于估计一个较为准确的初始近似根，在本问题中是求解下列方程的近似根y0。

$f(y)=y^{-2}-x=0$

快速平方根倒数算法利用了浮点数在内存中的映像格式，使用整数的移位和减法操作快速获取了方程的近似根y0，要明白 magic number 的原理，需要先了解浮点数在内存的存储格式。

IEEE754 浮点数存储标准

现代的计算机系统，几乎都是使用IEEE754标准来存储浮点数。单精度浮点数是32bit来表示的，它包括：

1bit：符号位。0表示这个数为正，1表示为负。
- 在本问题中x和y都是正数，所以推导过程中不用考虑。
8bit：幂运算的指数，对应的底数是2。
- 它可以表示0-255这256个整数，把它做一个偏移也就是减127，就是实际表示的指数。
23bit：尾数，表示一个符合科学计数法的小数。
- 想象在bit22之前有一个小数点，小数点前一位是数字1，小数点后面是一个二进制小数。也就是“一、点、加上后面这一串二进制小数”，它代表的值是1加上后面这些bit之和。其中bit22是最高位——表示1/2，后面的bit依次是1/4、1/8、1/16 ……

该内存映像表示的浮点数的值如此计算：

$\text {value}=(-1)^{\text {sign}} \times 2^{(E-127)} \times\left(1+\sum_{i=1}^{23} b_{23-i} 2^{-i}\right)$

$E=\left(b_{30} b_{29} \ldots b_{23}\right)_{2}=\sum_{i=0}^{7} b_{23+i} 2^{+i}=126$

$1. b_{22} b_{21} \dots b_{0}=1+\sum_{i=1}^{23} b_{23-i} 2^{-i}=1+1 \cdot2^{-2}=1.125$

$\text {value}=(+1 ) \times2^{-1} \times1.125=+0.5625$

后文会多次提到浮点数的内存映像和浮点数的值，请牢记并区分这两个概念，否则会带来理解上的障碍。

推理过程

回到原问题，稍作变换。用E表示指数、m表示尾数，E-127和m+1是它们分别对应的数值。

$y=\frac{1}{\sqrt{x}}=x^{-\frac{1}{2}}$

$x=2^{E-127} \times (1+m) \hspace{1cm} 1<=(1+m)<2$

把 x 代入第一个等式，可以得到 y 的准确值，它就是把 x 做了 -1/2 次方。

$y=2^{-\frac{1}{2}(E-127)} \times (1+m)^{-\frac{1}{2}} \hspace{1cm} 0.707<(1+m)^{-\frac{1}{2}}<=1$

我们的目标是：简单处理x的内存映像，从而直接获取y的近似值。设 y 的内存映像为

$y=2^{(E^{\prime}-127)} \times (1+m^{\prime}) \hspace{1cm} 1<=(1+m^{\prime})<2$

无论是 m 还是 m’ 都是 0-1 之间的一个数，直接用 m 表示 m’ 误差也不会太大。所以仅需探索如何用 E 近似表示 E’ （E 是已知的）。

根据前面的等式，显然有下面的近似等式成立。有了这个式子之后，就可以开始“神奇的魔法”了。

$2^{(E^{\prime} - 127)} \approx 2^{-\frac{1}{2}(E - 127)}$

$E^{\prime}\approx 190.5-\frac{1}{2}E$

回顾单精度浮点数内存映像格式：

现在讨论的是指数 E’ 和 E 的关系，所以可以把 IEEE754 格式的单精度浮点数当作整型对待，然后在 bit 级别进行操作，否则对它的任何操作都会变成浮点数的运算。所以在代码里才需要对这个浮点数进行非常复杂的 cast。

本质上算法想操作浮点数的内存映像，而不是浮点数表示的值。现在已知 E 的值，它就是输入的 x 的 exponent 部分。要通过 x 的 E 得到 y 的 E’，就是一个对整型的操作了，即E' = 190.5 - 1/2E。

下面这个计算，我们只关注 exponent 部分，我们希望把 E 变换成 E’。所以可以把这个 190 放到 exponent 的位置，让它变成一个常数，然后再减去 x 再右移一位（E除以2）。

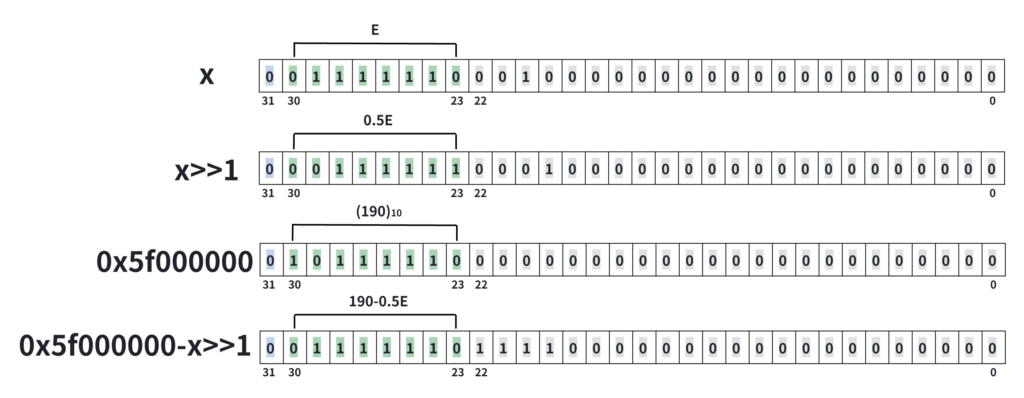
十进制的 190，对应的二进制是 10111110。

$E^{\prime}\approx 190.5-\frac{1}{2}E \approx 190-\frac{1}{2}E$

$(190)_{10}=(10111110)_{2}$

$y^{\prime}=\text{0x5f000000}-(x\gg1) \hspace{1cm}\text{Directly change memory image}$

整个操作里，压根没有考虑尾数，我们就是希望把 y 的 exponent 部分靠近需要的那个值，这里计算出的已经是一个估计值了，所以式子中用 y’ 来表示，与准确值 y 区分。

此时对比卡马克的原式，会发现二者已经非常接近了。

事实上，经过前述如此简单操作的 y’，已经是个不错的估计了

$0.71y<y^{\prime}<0.77y$

浮点数的值，和浮点数的内存映像对应的整数值，他们的关系是单调的。即内存映像的整数值越大，其表示的浮点数就越大（前提是 sign bit 为 0）。因为 significant 部分怎么加也不会超过 2，而 exponent 每多 1bit 就是 2倍。

由于这个良好的单调性，虽然 y’ 离准确值尚有差距，只需在 y’ 的基础上加一些 offset，就可以让它逼近准确值。算法中的 0x3759df 就是这个 offset，我觉得这个 offset 是试出来的。

发明这个算法的是一个程序员而不是数学家，遍历才是程序员的正常思维。
                                                                                                                                ——码农高天